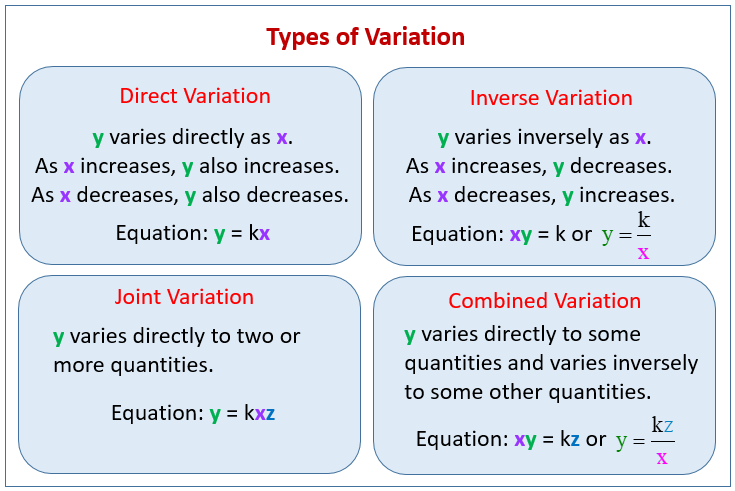
If more than two variables are related directly or one variable changes with the change product of two or more variables it is referred to as joint variation.
If X is in joint variation with Y and Z, it can be symbolically written as X α YZ. If Y is constant also then X is in direct variation with Z. So for joint variation two or more variables are separately in direct variation. So joint variation is similar to direct variation but the variables for joint variation are more than two.
Equation for a joint variation is X = KYZ where K is constant.
One variable quantity is said to vary jointly as a number of other variable quantities, when it varies directly as their product. If the variable A varies directly as the product of the variables B, C and D, i.e., if.A ∝ BCD or A = kBCD (k = constant ), then A varies jointly as B, C and D.
For solving a problems related to joint variation, first we need to build the correct equation by adding a constant and relate the variables. After that we need to determine the value of the constant. Then substitute the value of the constant in the equation and by putting the values of variables for required situation we determine the answer.