1.ANGLE BISECTOR LOCUS
An angle bisector locus is a locus of points equidistant from two fixed lines(AB and AC).
This locus is obtained by bisecting the angle formed between the two lines using the steps shown below.
- First,draw two lines AB and AC such that they form an angle at point A as shown in the diagram below.
- Place your compass at point A and draw an arc which crosses both sides of the angle.
- Using the same extension of your compass,place it on the two arcs crossing both sides and draw two intersecting arcs between the two sides of the angle.
- Finally,draw a line to pass through the point formed by the two intersecting arcs to point A.The line is the angle bisector locus as shown below.
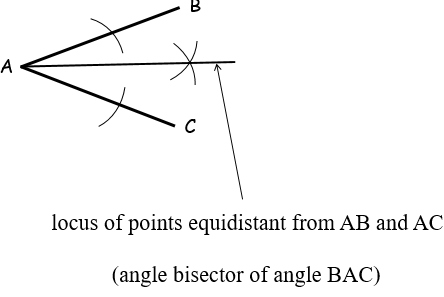
2. PERPENDICULAR BISECTOR LOCUS
This is the locus of points which are equidistant from two fixed points(A and B).
The locus is obtained by bisecting the line joining the two points using the steps given below.
- Firstly, draw a straight horizontal line and label either ends as A and B respectively.
- Secondly,place your pair of compass on point A and extend the compass so that it is positioned half way along the line.Using the compass, draw an arc along this half way point above and below the line.
- Whilst keeping the compass extended to the same length,position your compass at point B and an arc above and below the line.Locate the the two points where these arcs intersect.
- Draw a line joining these two points and you will have constructed the perpendicular bisector locus to line AB as shown below.
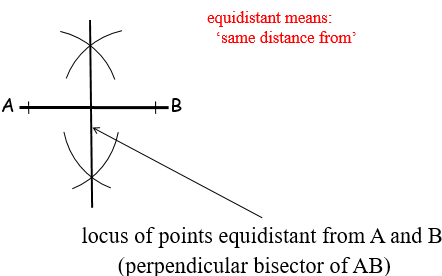
Note: You can check if your answer is correct by measuring the angle between line AB and the line constructed.If this angle is ninety degrees,then the two lines are perpendicular.