Pythagoras Theorem

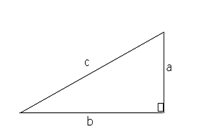
Pythagoras theorem states that for all right-angled triangles, 'the square on the hypotenuse is equal to the sum of the squares on the other two sides'. The hypotenuse is the longest side and it's always opposite the right angle.

In any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

i.e.: c² = a² + b² in the following diagram:

Example 1

Find AC in the diagram below.

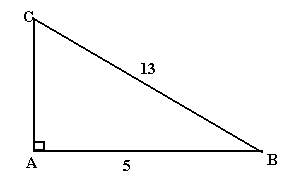
AB² + AC² = BC²
AC² = BC² - AB²
       = 13² - 5²
       = 169 - 25 = 144
AC  = 12cm

Example 2

A cuboid has sides of length 10cm, 2 √11 cm and 5cm. Find the length of a diagonal.

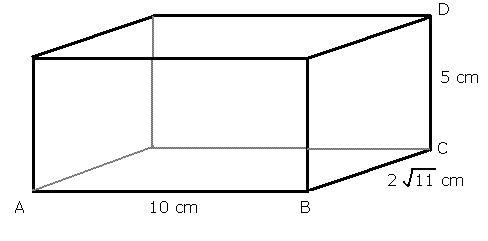
So we want to find AD.

We can draw a right-angled triangle inside the cuboid which has AD as it's hypotenuse. Then we can use Pythagoras.

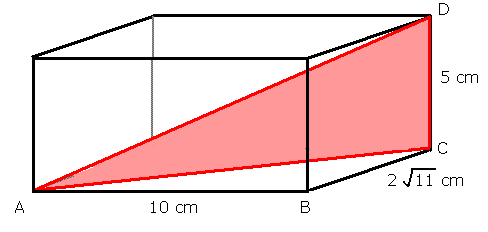
To use Pythagoras, we need to know AC and CD. We know that CD is 5 cm. We need to find AC.

We can use Pythagoras to find AC, because if we look at the cuboid from above, we see that AC is the diagonal of a rectangle.

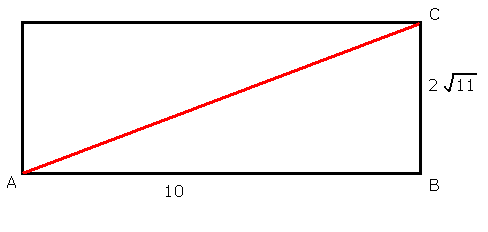
ABC is a right angled triangle, so by Pythagoras, AC² = AB² + BC²
= 10² + (2 √11)² = 100 + 44 = 144

Now we can find AD: AD² = AC² + CD² = 144 + 25 = 169
Therefore AD = 13

-Read the notes above and summarize the key points.

Outline the pythagoras theorem formulae