This Criterion for construction of Triangle is possible when the Hypotenuse and one side from the remaining two sides are known to us.

The requirements for the construction are a ruler and a compass. Let us construct a right-angled triangle ABC, right angled at C. Consider the length of the hypotenuse AB = 5 cm and side CA = 3 cm. The steps for construction are:

• Step 1: Draw a horizontal line of any length and mark a point C on it.

• Step 2: Set the compass width to 3 cm.
• Step 3: Place the pointer head of the compass on the point C and mark an arc on both the sides of C.

• Step 4: Mark the points as P and A where the arcs cross the line.
• Step 5: Set the compass width to the length of the hypotenuse, that is, 5 cm.
• Step 6: Place the pointer head of the compass on the point P and mark an arc above C.

• Step 7: Repeat step 6 from the point A.

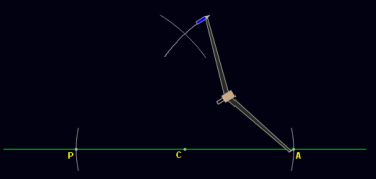
• Step 8: Mark the point as B where the two arcs cross each other.
• Step 9: Join the points B and A as well as B and C with the ruler.

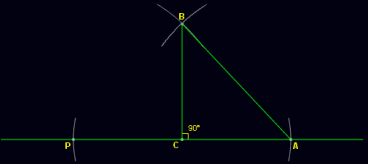
Thus, you obtain a right-angled triangle ACB of the required measurements.

Construct a right angled triangle ABC such that AB=5cm and BC=7cm right angled at B.